On December 9th I returned to the Trolley Barn to DJ again for my friend Valerie Young. This time around my goal was to have a better mix of high energy and lower energy “groovy” tunes, and I wanted to be better prepared for tying in endings at any time, no matter how many times through the caller requested.

Prep

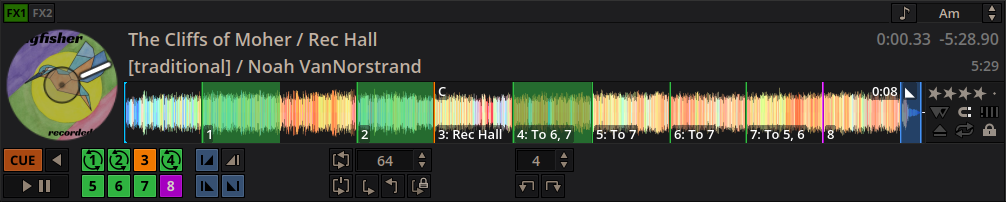
While I still prepped by marking each time through the dance with whether it looped cleanly or not, this time I (mostly) marked it with a cue instead of a 64 beat loop. I also named the cue based on what other cues I could jump to cleanly from it. For example, if I were on the last time through the dance I would mark if it looped cleanly itself, but also that I could jump backwards 3 times to cue 6 (or whatever the case may be). This way if I’m nearing the end of the dance but the caller is running it a bit longer I can reset without a single 32 bar phrase starting to get repetitive. I can also plan ahead by seeing that cue 6 lets me jump back to cue 8 or 9 afterwards (let’s assume these are the last two cues), which means that if the caller immediately calls 2 more times through I know that I can cleanly jump back to 2 more times without incident. I also mark a handful of things in the music such as if this time through the dance is a big recognizable build up (which I might not want to repeat even if technically it sounds okay), or if I shouldn’t jump back before a cue because the energy is significantly lower and we don’t want to kill the energy that had already been built up on the dance floor. This made it much easier to always follow the callers instructions and not have to scramble to wrap up the song or ask if we can do 4 times through the dance instead of 2 or what not.

The Set

I started out the set with a slowed down mix of “ Whelan’s ”, “ Baghad Gus ”, and “ Congress Reel ” all by Wild Asparagus. This was a medley that I had planned for my previous set but hadn’t managed to use, but it worked quite well to “ Whoever is Right is Right ” by Jim Hemphill. The only iffy moment I had in this medley was in one of the transitions where I thought I executed it perfectly, only to have the tune I was introducing jump half a beat ahead, breaking the rhythm. I had left the Quantize option on (which locks the two beat grids together even if you’re a little bit off) and unfortunately the beat grid on the song in question was about half a beat off at the point I was doing the intro.

Lesson learned: pay more attention to what options you’ve got selected (and reset them between songs, this would be a problem several times during the evening) and in a song where the beat grid can’t be right through the entire song (ie. because of tempo changes), make sure it’s correct at the point you’re going to mix in.

Whelan's / Baghad Gus / Congress Reel by Wild Asparagus, DJ mix

For the second dance Valerie picked “ Made Up Tonight ” by Erik Hoffman. This dance is relatively easy and in some ways similar to the previous dance so I decided the dancers could handle a little bit higher tempo and energy level. I did a mix of “ Bus Stop! ” by The Free Raisins and “ Rec Hall ” by Kingfisher. This is another mix I had prepared for my previous set and one of the ones I was most excited about performing. Unfortunately I completely broke the transition by just forgetting to bring the volume up on Rec Hall, so I ended up killing the music entirely for a few beats before I realized what was happening and brought it back in. It sounded terrible, and this one the dancers couldn’t help but notice, but Valerie kept calling so they were on beat still when I finally realized what was happening.

Lesson learned: go ahead and beat match and mix in a few bars early, then do the transition by bringing the volume up instead of just hitting play, or just remember to have the volume up first.

Bus Stop! / Rec Hall by The Free Raisins and Kingfisher, DJ mix

At this point Valerie decided to take the evening in a different direction from the modern, improper and becket contras that the Trolley Barn normally asks callers to stick to. She called “ The Steps of Waterloo ”, a traditional Sicilian circle, which I’ve never seen done at the Trolley Barn before. Since this one is both easy and a bit silly I used “[Flying Ice Cream]” by Giant Robot Dance which starts out very slow and groovy, then ramps up dramatically in the second half. Once the dance ramped up I mixed it with “ The Randomainians ” by The Great Bear Trio to make it last a little longer. This was the one mix and dance combo of the night that I was mostly extremely pleased with, when the tempo and energy ramped up half way through the song the dancers cheered and started frantically rushing to try and get to the basket swing in the limited time the (normally too fast) music allowed which was a lot of fun.

Lesson learned: prepare about twice as much music as you think you’ll need for the evening (to be fair, I already knew this, I was just struggling with the preparation for this set and didn’t end up with enough time to finish the other mixes I was considering).

Flying Ice Cream / The Randomanians by Giant Robot Dance and The Great Bear Trio, DJ mix

Continuing Valerie’s theme of not doing modern contras she picked “The Hand Jive”, a proper ceilidh, by Colin Towns next. Because this dance is a bit more “fun” and contains some patty-cake like hand games I decided to do a simple but fun mix of “ Raccoon ” by Wake Up Robin and Disco Snails by Vulfmon and Zachary Barker.

Unfortunately I hadn’t considered that, easy as the hand clapping is, it required Valerie to do a significant amount more calling than she normally would do and never drop out, so picking a song with lyrics was a bad idea. A few people still got a chuckle out of the “Disco Snails” cameo though.

Lesson learned: make sure to pay attention to how much the caller will have to talk and ask if they plan on dropping out before introducing something with lyrics.

Racoon / Disco Snails by Wake Up Robin and Vulfmon and Zachary Barker, DJ mix

We took our mid-dance waltz break at this point for which I played “ Waiting for Landfall ” by Julie Vallimont, “ Indifference ” by the String Beings, and “ Norwegian Reinlender / Schottis From Idre ” by Wild Asparagus. I’d hoped that some of the dancers would know the schottische for the second part of the medley, but mostly it just confused everybody who kept trying to waltz even though it was no longer a waltz.

Coming back we were running a bit late so I decided to drop the show-stopper for the evening, a mix of “ Rainy Night ” by The Dam Beavers, “ Tween Spirit ” by Giant Robot Dance, and “ Smells Like Teen Spirit ” (which, of course, the previous tune is a cover of) by Nirvana. This was paired with “ Birminghams ” by Gary Nelson.

I played the first two tunes as a normal medley, then when Valerie indicated that she was ready for three times left through the dance I mixed in the actual Nirvana version just for the ending. I was worried this crowd wouldn’t care for it, but when the tune first came in (as “Tween Spirit”) a lot of the dancers started singing along, and when actual Nirvana came in at the end the energy really ramped up and there was a lot of cheering and stomping, so apparently even the younger members of the crowd were still excited about 90s grunge!

The only real problem with this dance is that I had one moment where I had a clean loop that I wanted to repeat but as I did so some of the dancers, knowing what came next in the song, started singing the next verse and then had to stop when the music wasn’t what they expected.

Lesson learned: when doing a pop song don’t do transitions that would break the progression of the song that people are already used to, even if they sound okay.

Rainy Night / Tween Spirit / Smells Like Teen Spirit by The Dam Beavers, Giant Robot Dance, and Nirvana, DJ mix

At this point I realized that I hadn’t prepared enough mixes for the dance and I was more or less out of material. For the next one Valerie asked to do a very short square dance, the “ Cumberland Square Eight ”. Since it was going to be so short and timing didn’t matter I played “ Heather’s Concussion ” by The Great Bear Trio without mixing it into a medley.

This tune is itself very short (only three times through) and far too fast for a normal contra, so I slowed it down (though still keeping it too fast) and sped it up slowly through the dance to mess with the dancers. They looked like they had a good time!

Heather's Concussion by The Great Bear Trio, DJ mix

This left us with just enough time for a no-walk-through contra. I had nothing else prepared but wanted to send us out on an easy-tempo dance after the various fast shenanigans from the rest of the night, but still have some good energy. I dug around in my library and ended up playing “ Apple Blossom ” by Great Bear. Since I didn’t have anything to mix this with I just played it through and looped once or twice near the end to keep the high-energy ending going. The dance Valerie picked was an easy ending dance that is unfortunately called “Unnamed Contra” and she didn’t know who wrote it.

Apple Blossom by Great Bear, DJ mix

We then closed down the evening (very late, much to the chagrin of the organizers) with “ Mending ” by “The Little Mercies”.

Stuff I Learned

A recap of the things I need to take away from the evening:

• Be thoughtful about resetting all controls, levels, mixing, effects, etc. between tunes. Possibly write down the initial state for each song so that you can re-set the board at a glance.
• Beat match early then use the volume sliders for transitions, don’t just start playing immediately at the entry point (or just remember to turn up the volume as you approach the mix point).
• Consider how much the caller will have to talk in any given dance and how soon they’re dropping out before mixing in vocals.
• For pop songs, don’t violate the order of the verses or breaks that people expect, even if the final result sounds okay. It’s jarring for the dancers who are used to it being a certain way.

And finally: relax and enjoy it! While I spend the entire evening worrying about how the sound dropped out for a moment, or my transition was a beat off and I saw the dancers stumble and catch back up, or whatever other disaster might have befallen, no one remembers any of that. I got a very nice message from the organizer the next day telling me how excited everyone was and how many conversations she’d had with people telling her how much they enjoyed the music!

Other Links

• The set list on MusicBrainz
• Recordings of the evening can be found on the Internet Archive

Erlang Solutions launched SAFE, a Security Audit for Erlang in the fall of 2023. We extended the analysis for Elixir in the spring of 2024 and now, SAFE officially supports Phoenix Liveview, which means a SAFE scan is now looking for vulnerabilities common in Phoenix web applications.

What is SAFE?

SAFE is a security scanning tool for Erlang, Elixir and Phoenix (LiveView) codebases. It works by loading and analysing your code, without running it. SAFE conducts an in-depth analysis of codebases, which can help you and your company to elevate your cybersecurity.

Supporting Phoenix LiveView

Now, as of the 1.3.0 release of SAFE, we support Phoenix LiveView, which means we can check for the following vulnerabilities:

• Cross Site Scripting (XSS)
• Cross Site Request Forgery (CSRF)
• Cross-Site WebSocket Hijacking (CSWSH)
• SQL Injection (with Ecto support)
• Denial of Services (DoS)
• Session leakage (unprotected session information)
• Session fixation (session ID renewal issues)
• Session hijacking
• Content Security Policy (CSP)

On-Prem report visualisation

With the release of the new SAFE version, a new SAFE product flavour was also launched, called SAFE OnPrem. This solution allows companies to host a centralised security report viewer that engineers and security specialists can access via the web interface.

Overview page of an example report:

User management:

Running SAFE

If you are interested in running SAFE on your code base, please check out our Quick Start Guide and contact the SAFE team . You can also drop us a message if you maintain an open source project, as you may be eligible for a free SAFE license.

More information about Open Source licensing can be found in our announcement blog post .

The post SAFE for Elixir: Phoenix LiveView appeared first on Erlang Solutions .

Signal improved its protocol to prepare encrypted messaging for the quantum era.

They call the improvement “Triple Ratchet” (or SPQR = Signal Post-Quantum Ratchet).

If history repeats itself, this could become the next open standard for secure messaging.

Signal (formerly Open Whisper Systems) created the Double Ratchet protocol in 2013–2014, introduced in TextSecure v2 in February 2014. They packaged it into the open source Signal Protocol. It became the mainstream standard for end-to-end encrypted messaging. XMPP adopted it (OMEMO, developed in 2015). Matrix adopted it (Olm/Megolm implements Double Ratchet concepts).

The problem is that current encryption methods could break when quantum computers get powerful enough, so Signal built Triple Ratchet to protect against that.

Most messaging companies are preparing for this but I noticed that WhatsApp has no public roadmap for the adoption of quantum resistance protocols. They use the Signal Protocol for encryption, so they may simply wait for the result of Signal’s work to adopt the new approach.

It is much heavier to implement, so I am wondering if Triple Ratchet follows the same path as Double Ratchet and gets widespread adoption.

If open protocols like XMPP and Matrix adopt it, it may be huge for European messaging independence.

What’s your take? Do you think quantum resistance will become a mandatory feature for end-to-end encrypted messaging platforms in the next couple of years?

Esports has outgrown local tournaments and now runs on global platforms linking millions of players and fans, powered by immersive esports technology . Communities form around games, teams, and streamers, blending competition, entertainment, and social connection. At this scale, reliability and low latency are non-negotiable to keep matches fair and audiences engaged during spikes.

High-speed networks, cloud rendering, modern graphics, and streaming make worldwide play possible, while data and AI sharpen strategy. Crucially, infrastructure must scale horizontally across regions, cache at the edge, and expand automatically under load so performance stays consistent.

This article maps the technologies behind modern esports and the design choices that keep them resilient at scale, so the experience feels instant from first click to final play.

The Global Picture

Let’s start with the big picture and why esports now feels like a shared live moment wherever you are.

You may have watched a finals stream with friends or shared a highlight in chat. That everyday moment sits on top of a vast market and audience. The market has expanded at a 20.9% rate in recent years.

Source: Scoop Market

The global esports audience surpassed 500 million viewers in 2020 . Industry revenue reached around USD 2.0 billion in 2023 and is projected to grow to USD 5.5 billion by 2029. Longer-term forecasts suggest a compound annual growth rate of nearly 21%, with revenues expected to reach USD 10.9 billion by 2032 .

Esports is digital-first, so fans join live from different regions at the same time. That reach shapes every technical choice.

Platforms and Real-Time Infrastructure

Fans expect more than a broadcast. They want to react, interact, and feel part of the match. Meeting that expectation means processing actions and reflecting results in milliseconds: bets settle as they happen, moves register for every client at once, and streams stay in step with in-game events.

Behind the scenes, persistent connections keep two-way communication open. Load balancers and game servers handle traffic and core logic. Event-driven patterns broadcast only what each user needs. Caching and in-memory stores such as Redis answer hot reads quickly. Content delivery networks ( CDNs) and edge locations reduce round-trip time for global audiences. These are the building blocks of immersive esports technology , and they exist to keep the experience responsive when traffic surges.

Speed protects immersion and trust. A delay during a clutch play or a live bet breaks both. Real-time platforms enable instant feedback, live chat, synced multiplayer, and up-to-the-second odds. Operators benefit as well: live data supports fraud checks, personalised offers, dynamic pricing, and timely promotions. The result is higher retention and fairer play.

AI and Data: From Play to Shared Insight

This is where raw play turns into insight that helps players, teams, and viewers get smarter together.

Artificial intelligence (AI) now supports training, planning, and engagement across the community. Teams review footage with machine learning, spot errors, and test scenarios before match day. Virtual assistants help track progress and suggest adjustments.

Matchmaking pairs players of similar skill so every game feels balanced, while anti-cheat tools monitor play in real time and respond within seconds. For viewers, AI compiles highlights, personalises feeds, and surfaces stats that spark discussion. AI does not replace the human side of esports. It amplifies it by making fair play easier to maintain and shared learning easier to access.

The Future of Immersive Esports: AR, VR, and Cloud Integration

Next, we look at how new realities and cloud power will make watching and playing feel more present.

Esports is moving toward presence, not just pixels. The next wave blends virtual reality (VR), augmented reality (AR), and cloud, so players and fans feel inside the match while platforms hold steady under load.

At a basic level, cloud rendering sends high-quality visuals from powerful servers straight to headsets and phones, so devices do less work and the action feels smooth. Nearby servers cut the time between your input and what you see, which means steadier aim, smoother movement and viewers who stay in sync with the match.

On the viewing side, augmented reality (AR) adds simple overlays like live stats, heatmaps and quick point-of-view switches for watch parties. Fans can pin tactics on screen and share clips that include useful context, not just the video. For collaboration, social virtual reality (VR) creates shared rooms where teams review rounds together, coaches sketch ideas in space, and gentle haptic cues help with timing. Early brain-computer interface (BCI) research is already improving training and accessibility, with competitive use further out.

Operationally, security and identity are handled in the cloud. Anti-cheat updates roll out quickly, and your profile and items travel with you across devices. Better compatibility between platforms helps communities stay together wherever they log in.

Cloud rendering, AR, and VR stitched to edge-first delivery keep the play responsive and viewing in sync at any scale. The technology fades into the background, matches feel immediate, spectators feel present, and communities stay connected long after the final round.

Scalability in Esports Platforms

All of this only works at scale, so these are the principles that keep things smooth when the crowd shows up.

Immersive features raise the bar. AR, VR, and cloud expand access, lengthen sessions, and multiply real-time events. To keep the experience smooth, platforms must scale from the first click to the final play.

Design principles

Scale out horizontally rather than relying on larger single servers. Hold latency steady as traffic rises. Use distributed services that add capacity on demand. Place compute at the edge to shorten round-trip times for inputs, tracking, and streams. Move events through queues and pub/sub so spikes do not reach clients. Share hot data. Cache reads close to players. Isolate failure with circuit breakers and graceful fallbacks.

Consistent experience under load

Keep match starts fast, frame timing stable, chat responsive, and spectating in sync during peak traffic. Run multi-region deployments with smart routing so performance feels similar across continents. Maintain identities, inventories, and anti-cheat on the server and keep them in sync across devices.

Operate by signals

Define SLOs for latency and availability. Instrument everything. Auto-scale from real usage, not guesses. Use rolling updates, redundancy, and automatic failover to stay always on. Control cost with elastic capacity that expands for events and contracts afterwards. This is where immersive esports technology proves its value, turning peak moments into reliable moments.

Proof in production

Scalability is the test that decides whether real-time features, AI-driven insights, and AR/VR hold up. Peak moments create sudden spikes in concurrent users, messages, and state updates. A scalable platform keeps latency steady, expands capacity on signal, and degrades gracefully if a region falters.

FACEIT shows what this looks like in practice. Working with Erlang Solutions , the team upgraded MongooseIM and Erlang, redesigned presence at scale, and tightened deploys. The result was a two-times speed increase and stable support for up to 250,000 users with lower maintenance. Crucially, presence and chat stayed responsive during surges, which is the hallmark of a platform built to scale rather than cope.

In the end, scaling well turns pressure into proof. When capacity grows on signal and services degrade gracefully, peak moments feel natural, competition stays fair, and communities keep turning up. That is how the tech steps back and the match takes centre stage.

To conclude

Esports thrives when technology fades into the background and the community takes centre stage. Real-time services keep playing responsively. AI and analytics turn activity into shared insight. AR, VR, and cloud widen access. Scalability makes peak moments feel natural. If you are building or scaling an esports platform, design for low latency and resilience from day one. We design real-time systems that keep matches responsive and communities connected, so get in touch .

The post Immersive Esports: The Technology Behind Competitive Gaming appeared first on Erlang Solutions .

Joining conferences is one of the best perks of working as a Developer at Erlang Solutions. Despite having attended multiple Code BEAM conferences in Europe, ElixirConf US 2025 was my first. The conference had 3 tracks, filled with talks from 45+ speakers and 400+ attendees, both in-person and virtual.

ElixirConf is one of the great occasions to connect with other Elixir enthusiasts in the community and get to learn what others have been doing as well as what the Elixir core team is planning for the future of the language.

The Atmosphere

Most of the faces were unfamiliar to me, but as expected from the BEAM community, everyone was super friendly. Most were not shy about approaching others, sharing about their own or their company’s experiences. The “hallway track” was always lively during the coffee break or during the talks.

Before the conference began, I had a tough time deciding which talk to attend. At other conferences I’ve been to, most of the talks were interesting, but not all were relevant to my daily work as an Elixir developer. That made it easier to prioritise which talks to attend live and which ones I could catch up on later if they overlapped.

ElixirConf was different. Many of the talks were not only interesting but also directly relevant to my work, and several were scheduled at the same time. This made it very difficult to decide which session to attend in person and which to leave for the recordings.

Some standout talks

Chris McCord’s Keynote: Elixir’s AI Future

One of the talks I was most looking forward to was the keynote by Chris McCord. I had previously watched the recording of his ElixirConfEU keynote about phoenix.new and was eager to see what new ideas he would bring to Elixir and the Phoenix framework, especially in terms of AI.

Chris talked about AI agents, how Elixir is well-suited for building them, and what the future of Elixir and AI might look like. He emphasised that it is not about chasing hype but about staying on the bleeding edge of technology: “building the things we want to build, building the things we want to see.”

He also shared his perspective on code generation, noting that it has made it easier for newcomers to get started with Elixir and Phoenix. In his view, the community is now in a strong position to attract developers from outside the ecosystem to give it a try.

Panel: Building Careers, Balancing Life

Another talk I was eager to hear was the panel discussion hosted by my Erlang Solutions colleague Lorena, together with Allison Randal, Savannah Manning, and Anna Sherman, three women from different backgrounds and stages of their careers.

It was great hearing stories from other women in the tech community and feeling inspired. The three panellists shared the stories and challenges they had faced in their careers. They also talked about the importance of having mentors, the community, and knowing the big picture, which helped them grow. The advice they gave during the talk was both very relatable and inspiring.

Joe Harrow: Beyond Safe Migrations

I also found Beyond Safe Migrations to be great food for thought. This talk was a very practical and solid example of what could go wrong in a live database migration, and the tool Cars Commerce was using to prevent that. Over the span of my career, I have written many database migrations, from small startup projects altering a table with only a few hundred rows to large-scale projects where the tables had millions of rows.

My team sometimes discussed strategies for altering existing tables, but most of the time we would just go ahead and make the changes. Listening to Joe, I learned about things that could have gone really wrong and that there is a systematic way of mitigating those risks.

Key Takeaways

All in all, Elixir Conf US was a great conference, packed with talks about experiences and challenges, new and upcoming technologies, and also about growing the community. There was, of course, a surge in AI-related talks, both from early adopters to the future of Elixir with AI.

I found that the main theme running through the conference was the growth and sustainability of the Elixir community. ElixirConf is well worth attending, whether you are just starting out or already an experienced developer.

The post ElixirConf US 2025: Highlights from My First ElixirConf appeared first on Erlang Solutions .

Last week, Spotify quietly launched direct messaging across its platform in selected areas, allowing users to share tracks and playlists through private conversations within the app. The feature was rolled out with minimal fanfare but significant media coverage, positioning itself as a complement to existing sharing mechanisms through Facebook, WhatsApp, and TikTok.

When I read this, I immediately wondered why they were bothering. We do not especially lack communication channels these days. So, Let’s take a step back and examine what Spotify is actually trying to accomplish here.

The Strange Case of Another Messaging App

We already have too many messaging apps to choose, either on mobile or mobile phones. Before I try to initiate a conversation with someone I do not often chat with, I find myself trying to remember what is her preferred messaging platform. So, adding to an app some sorts of real time messaging and live interaction features can bring value, but it has to serve a purpose and respond to some user needs.

In that context, Spotify’s decision to roll out direct messaging support feels odd. Users can already share music through established platforms where their friends actually are. They can post discoveries on social media, send links through WhatsApp, or create collaborative playlists. Why would anyone choose to message someone specifically within Spotify when they’re already connected elsewhere?

The problem is that Spotify failed to make a compelling argument for why users should discuss with friends through yet another messaging system, even if this is to talk about music. Launching a special purpose communication service is risky. When Apple Music attempted to build Ping, a social network of music fans, it failed spectacularly. Spotify’s own social experiments haven’t fared much better. Remember Greenroom, their audio-focused social platform that quietly disappeared?

This initiative becomes even more puzzling when we consider Spotify’s own history. The company built its initial viral growth through Facebook integration, leveraging social connections to drive adoption.

And now, seemingly, they are trying to reclaim that social layer for themselves?

What’s Really Happening Under the Hood

The technical implementation reveals interesting choices. According to available reports, the messaging system relies on a RESTful API over HTTPS with TLS 1.3 encryption and JSON Web Tokens for session authentication. Notably absent? End-to-end encryption.

And this absence tells us that the feature is not considered as a standard messaging service yet, but simply an alternative way to share favorite tracks and discuss them, and a possible a move to reduce the amount of data exposed to other social networks and messaging.

The Data Intelligence Play

Messaging features can provide enormous value when you have a strong daily user base, but only when they address a clear user need. Spotify’s messaging doesn’t seem designed for users. It feels designed for Spotify’s recommendation algorithms.

Every shared track, every reaction, every conversation thread becomes a new data point in Spotify’s machine learning models. Who shares what with whom? Which songs generate discussion? How do musical tastes spread through social networks? This intelligence is pure gold for a recommendation engine that already struggles to compete with YouTube Music’s discovery capabilities.

Private messaging amplifies this data collection while keeping the intelligence proprietary, unlike public social sharing, where competitors might also benefit.

Strategic Confusion or Calculated Move?

So, is this really all about data collection and control?

This is where Spotify’s European identity becomes relevant. As a Swedish company competing against American tech giants, there may be strategic value in reducing dependence on US or controlled Chinese social platforms. Every track shared through WhatsApp (Meta) or TikTok (ByteDance) represents data flowing to potential competitors or partners with their own agenda.

Building an internal messaging system allows Spotify to capture that social intelligence directly while reducing what they share with other platforms. From a data sovereignty perspective, this makes sense, especially for a European player navigating an increasingly fragmented global tech landscape.

And they may hope at some point to play a larger role in messaging platforms in general, as we deeply miss a large player in the messaging field in Europe. It may be a play to test the waters.

As we help companies reclaim their independence by building their own messaging service, this goal resonates strongly with us. However, building a successful messaging platform requires being able to create momentum around the service if it wants to attract enough users and traffic. It cannot be launched halfheartedly.

The Missing Strategic Vision

The fundamental problem isn’t technical. It’s strategic clarity. Spotify has a recommendation engine that could benefit from social signals, a creator platform focused on podcasts and videos, and a user base that already shares music socially. The ingredients for a compelling set of social features exist.

But launching messaging without addressing the basic question of “Why would I message someone here instead of where we already talk?” suggests a feature developed in isolation from user needs. It resembles the countless platform features that launch with media coverage but die quietly when adoption numbers disappoint.

What would make this feature compelling? Integration with Spotify’s creator tools, perhaps allowing artists to connect directly with fans. Or collaborative listening live sessions where messaging enhances shared musical experiences. Or leveraging Spotify’s podcast ecosystem to enable discussion around episodes.

Instead, we get generic messaging that competes with platforms where users’ friends actually are.

So, what’s Spotify’s real goal?

I see two possible options here: a pessimistic and a more optimistic one.

Perhaps the most interesting aspect of this launch is what it reveals about Spotify’s growth concerns. A mature platform doesn’t typically add generic social features unless it’s worried about engagement metrics or looking for new growth vectors.

They may want their users to spend more time in its interface, instead of most of the time, passively using that app through a player exposed as a widget in the mobile operating system.

The timing suggests Spotify sees either limited growth ahead or a competitive threat that requires better user data. Given the AI revolution in music generation and the ongoing battles over royalty structures, capturing more nuanced data about user preferences and social music behavior could be crucial for maintaining relevance.

But there’s a more optimistic reading: this could represent a European tech company trying to assert more independence from American social platforms. In a world where data is power, controlling your own social graph has strategic value.

The execution, however, suggests Spotify hasn’t quite figured out how to articulate this vision to users. Until they do, this messaging feature risks joining the graveyard of platform additions that made sense to product managers but never found their audience.

In a world already oversaturated with communication channels, every new messaging system needs to answer a simple question: Why here instead of everywhere else users are already talking? Spotify hasn’t answered that question yet.

This new version includes a few new XEP plugins as well as fixes, notably for some leftover issues in our rust JID code, as well as one for a bug that caused issues in Home Assistant.

Thanks to everyone who contributed with code, issues, suggestions, and reviews!

Healthcare is moving quickly, and technology is playing a big part in that shift. The way information is collected, the way patients are cared for, and the way hospitals run are all changing.

Over the past year, our team has written about some of the most important trends shaping the future of healthcare. In this round-up, we bring together three of those articles: remote patient monitoring, big data, and generative AI.

Maybe you have been following along, or maybe one or two of these slipped past you. Either way, this is a chance to catch up on the ideas that are influencing healthcare right now.

What is Remote Patient Monitoring?

Remote Patient Monitoring (RPM) is already changing everyday care. With the help of connected devices, clinicians can see what’s happening with patients at home, step in earlier when something changes, and prevent unnecessary hospital stays.

“ What is Remote Patient Monitoring? ” sets out how RPM works, the devices that make it possible (from blood pressure monitors to smart inhalers), and why it is now a priority for healthcare leaders. The article shows how RPM is transforming chronic disease management, post-operative recovery, elderly care, and clinical trials, while driving down system costs by up to 40 per cent.

Digital care models like virtual wards are no longer experiments. They are reshaping the NHS and health systems worldwide, and this guide explains why.

Understanding Big Data in Healthcare

Healthcare produces enormous amounts of information every day. Patient records, medical scans, wearables, and research all add to the mix, and the real challenge is turning it into something useful. Done well, big data can improve care, reduce costs, and even speed up medical breakthroughs.

“ Understanding Big Data in Healthcare” breaks down the fundamentals, including the three V’s that define it: volume, velocity, and variety. You’ll see how providers are already using data to personalise treatments, predict health trends, and cut readmissions by up to 20 per cent. The article also shows how it can shorten clinical trial times by 30 per cent and reduce costs by as much as 50 per cent.

But with opportunity comes risk. The average cost of a healthcare data breach now stands at $9.77 million, making security a top priority for every provider. The article looks at the biggest threats, the regulations shaping data use, and how technologies like Erlang, Elixir, and SAFE can help keep information secure and systems reliable.

How Generative AI is Transforming Healthcare

With adoption already valued at more than $1.6 billion, generative AI is fast becoming one of the biggest drivers of change in healthcare. The global AI in healthcare market is projected to hit $45.2 billion by 2026, reflecting the scale of its potential to improve patient outcomes, support clinicians, and make systems more efficient.

In “How Generative AI is Transforming Healthcare” , we look at how it differs from traditional AI and why its flexibility makes it such a powerful tool for the industry. The article explores real-world applications such as personalised treatment plans, predictive analytics, enhanced diagnostics, virtual health assistants, and even accelerating drug discovery.

It also considers the future of AI in healthcare, including the need to address challenges around privacy, regulation, and patient trust. With the right planning and technologies like Elixir supporting scalable and reliable systems, generative AI could help shape a new era of patient-centred care.

To conclude

That wraps up our latest healthcare round-up. We hope this guide helps you cut through the noise and get a clear picture of the trends that matter most right now.

If something here has sparked your interest, whether it’s the possibilities of remote monitoring, the power of data, or the promise of generative AI, we would love to keep the conversation going. So get in touch .

Here’s to smarter systems, healthier outcomes, and more confident decision-making in healthcare.

The post Healthcare Blog Round-Up appeared first on Erlang Solutions .